不是什么摆法都能用一辈子。不求天长地久,但求曾经拥有。
很多朋友已经习惯了无敌摆法,但是它有一个很大的缺点,必须在紧靠厨柜的那一排摆放桌椅。这里给出的另一种满效率摆法,则没有这个限制。
这种摆法并不是最新发现的。在无敌摆法公布的同时就已经被发现了(背靠背就是一典型应用),但是这么长时间以来一直没有对这个摆法的详细介绍。前两天潞潞的研究再次证实了这一摆法的可行性。
示例
下图2厨10服,可以达到满效率(27级以上)。

为了方便说明,首先临时给出几个定义(仅在本文中有效)。
有效桌椅:服务员能从桌子上菜的桌椅。如图中的黄色桌椅和绿色桌椅。
无效桌椅:服务员只能从椅子上菜的桌椅。图中所有灰色桌椅都是无效桌椅。一个桌子呈正方形,有四个边,其中一边是椅子。如果把另外三边都用装饰或桌椅档住,它就成了无效桌椅。
死桌:服务员不论从桌子还是椅子都无法上菜的桌椅。装修时,这样的桌椅通常会变成红色,不停地闪烁。
服务员只能从靠近厨柜的那一排从左数起的第3、4、5、6、7、8这6个位置上菜。如果第3个位置没有被挡住,那么服务员通常就从第3个位置上菜。考虑从这个位置出发,走到所有的有效桌椅,计算最远的那个桌椅的距离。上图中,绿色桌椅比黄色桌椅远,其距离是13格。27级以上,只要满足这个距离不超过14格即可满效率。
摆法说明
只要使有效桌椅距离厨房尽可能近,桌椅总数(有效桌椅+无效桌椅)尽可能多,服务员尽可能多,就能达到满效率。
顺便说一下,无敌摆法之所以“无敌”,是因为它只有一个有效桌椅,而且离厨房最近。
厨房距离最远有效桌椅的距离必须满足的格子数条件。
|
15至16级,不超过12格 |
常见问题
1、什么是满效率?
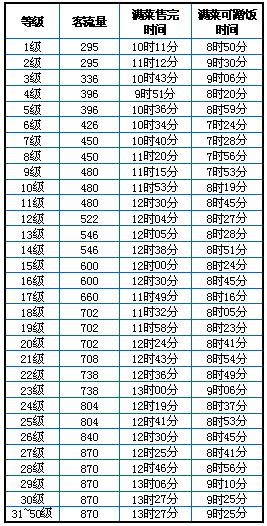
每个等级都有一个系统规定的客流量,如果主菜的卖出速度等于客流量,即为满效率。比如,30级的客流量是870人/小时。也就是说1个小时有870个客人来吃饭。如果主菜每小时能卖出870份,让每个客人都有菜可吃,就表示达到了满效率(注:一个客人只吃一份主菜)。不论如何装修,如何雇佣雇员,都不可能使主菜的售出速度超过满效率时的速度。文末附上满效率的时间对照表。
2、我二个服务员就已经满效率了,还需要再雇佣服务员吗?
应该努力雇佣尽可能多的高加成雇员。因为达到满效率,只表示主菜的出售速度达到了极限,并不表示挣得的金币和经验也达到了极限。雇佣有加成的雇员,可以获得金币加成和经验加成。加成的效果可以累加。比如雇佣10个小五(5%加成的雇员),加成就有50%,这意味着你挣经验的速度比没有加成时快一半。
3、有效桌椅是越多越好吗?
不一定。只关心最远的那张有效桌椅到厨房的距离。
4、有效桌椅距离厨房越近越好吗?
取决于对装修美观的要求和雇佣服务员的数量。最远那个有效桌椅距离厨房越近,就表示可以请越少的服务员就能达到满效率。如果距离1个或2个格子,就只需要请2个服务员即能满效率。
5、本摆法对桌椅总数有什么要求?
桌椅数(包括无效桌椅)越多越容易达到满效率。如果没有达到满效率,请尝试增加桌椅数量。通常情况下需要至少10到14桌。专业地说,桌椅的最少数量是由等级和最远餐椅到大门的距离这两个因素所决定的。
6、厨师要多少个合适?
一个厨房1小时能做出450份菜。2个厨师1小时能做出900份菜,已经超出了满效率时的速度,所以,请2个厨师足够。当然,如果雇员总数足够,多请厨师也没坏处。
7、本摆法比起无敌摆法有什么优势?
紧靠厨房的那一排不需要摆放桌椅。
8、待添加。
满效率时间对照表